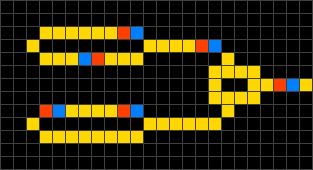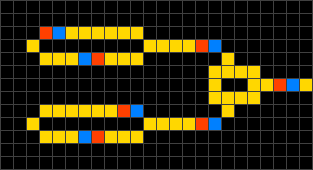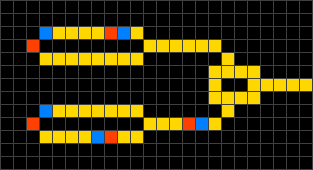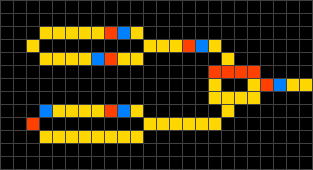PYTHON : PROJETS 2025
Tous les projets proposés sur cette page mettent en oeuvre la réalisation d'une
application complète, qui inclut à la fois des entrées/sorties sur fichier (par
exemple pour stocker la configuration d'un jeu ou le tableau des meilleurs
scores) et une interface homme/machine pilotée au clavier et/ou à la souris.
Ces projets vont donc nécessairement avoir besoin d'un certain nombre de modules
de la bibliothèque standard fournie avec le langage Python.
Avant de commencer, il est donc très utile de bien étudier et comprendre
l'ensemble des codes sources fournis dans les exemples vus en cours, ainsi que
dans les solutions des exercices vus en TD, qui fournissent des points de
départ pour le code à réaliser. En particulier, l'utilisation des modules
ezCLI et ezTK est OBLIGATOIRE car cela va vous permettre
de gagner beaucoup de temps sur la réalisation et la finalisation du code. Pour
chacun des sujets, sont indiqués les exemples et les exercices qui pourront
vous servir de point de départ.
A partir de la semaine 19 (5 mai), la moitié créneaux de TD seront exclusivement consacrés au suivi
du projet de programmation. Il est donc primordial que les 2 membres du binôme soient
présents simultanément. Si les 2 membres du binôme ne sont pas officiellement dans le même
groupe de TD, on organisera une permutation spécifique pour les créneaux concernés, en
fonction du nombre de binômes concernés. La présence à ces séances de suivi est OBLIGATOIRE
et toute absence non justifiée sera fortement sanctionnée par une pénalité d'un tiers par absence
sur la note finale du projet (coefficient 0.66 pour une absence, 0.33 pour deux et 0 pour trois).
Projet 1 : Rush
Ecrire un programme rush qui implémente une
variante du jeu Rush Hour, disponible sur différents
sites web ainsi que sur téléphone Android ou iOS (sous les noms "Rush
Hour", "No Parking", "Traffic Rush" ou "Traffic Jam"). Le jeu se joue sur une
grille 6x6 simulant un parking où se trouve des voitures (rectangles de 2 cases
alignées) ou des camions (rectangles de 3 cases alignées). L'objectif du joueur
est de faire sortir la voiture rouge du parking en déplaçant les autres
véhicules (en avant ou en arrière) pour ménager un chemin vers la porte de
sortie.
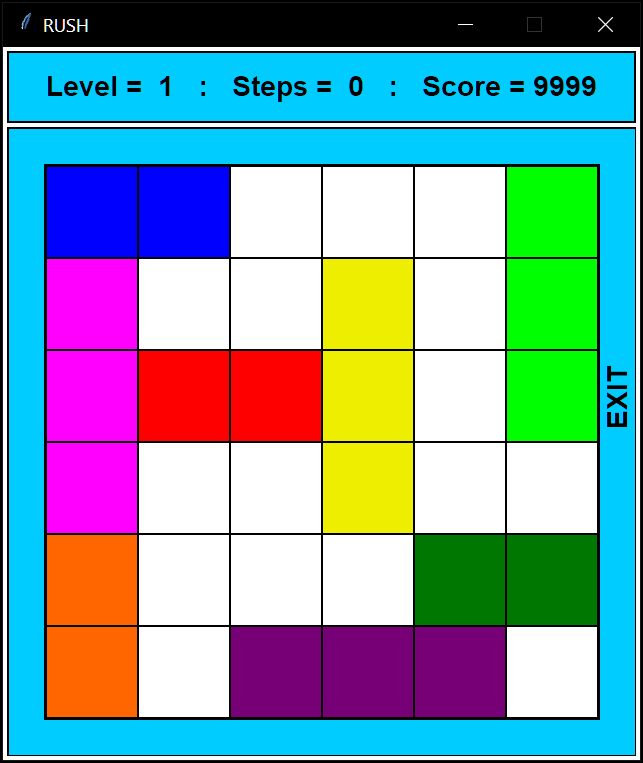
Dans la variante demandée pour ce projet, le graphisme est simplifié à
l'extrême en définissant de simples cases de couleur pour identifier les
différents véhicules (cf. image ci-dessous), mais évidemment rien ne vous
interdit de mettre en oeuvre une visualisation plus élaborée. Le haut de la
fenêtre affiche une zone d'information avec les 3 paramètres du jeu : le numéro
du niveau en cours, le nombre de déplacements effectués pour ce niveau, et le
score courant du joueur. Le jeu devra se piloter à la souris selon les mêmes
modalités que la version présentée dans le lien ci-dessus: cliquer sur
l'extrémité d'un véhicule le fait avancer d'une case dans cette direction. Pour
chaque niveau, le programme devra détecter le moment où le chemin vers la sortie
est dégagé pour la voiture rouge, et lancer une animation qui déplacera
automatiquement la voiture pour la faire sortir du parking.
Le jeu utilise un principe de score décroissant pour évaluer les performances
du joueur. Au départ, le joueur possède 9999 points et chaque déplacement d'une
case pour un véhicule, lui fait perdre un point. L'objectif est d'arriver au
bout des 40 niveaux du jeu en ayant consommé un nombre minimal de points de
déplacement. De manière optionnelle, on pourra également rajouter un mécanisme
de renoncement : si le joueur n'arrive pas à finir un niveau, il peut cliquer
sur la ligne de score en haut de la fenêtre, pour passer directement au niveau
suivant, en acceptant de prendre ainsi 100 ou 200 points de pénalité.
Pour simplifier le développement du programme, on fournit une archive
rush.zip qui contient un fichier CSV
regroupant 40 grilles classées par niveau de difficulté, ainsi qu'un fichier
squelette rushZ.py qui pourra servir de point de départ pour
l'implémentation. La lecture du fichier CSV et sa conversion en un tableau
de chaînes de caractères sont déjà inclus dans le squelette.
Exemples à relire avant de commencer le projet :
- Exemple C6B_event.py et Exercice C5A_leapfrog.py (pour la gestion
des clicks de la souris)
- Exemple C4C_random.py (pour l'utilisation de la widget Entry)
- Exemple C2C_toggle.py (pour la mise en oeuvre de l'animation de la
voiture rouge)
- Exemple B4A_csvfile.py et Exercice C6A_maze.py (pour la lecture des
fichiers CSV)
Projet 2 : Flood
Ecrire un programme Flood qui implémente une
variante à 2 joueurs du jeu Food-It, disponible sur différents
sites web ainsi que sur téléphone Android ou iOS. Dans le jeu
standard à 1 joueur, l'objectif est de colorier l'intégralité de la grille
en une couleur unique, en partant du coin supérieur gauche et en inondant
toutes les cases connexes de la même couleur. A 2 joueurs, le jeu se
transforme en une conquête territoriale, où l'objectif de chaque joueur est
d'être le premier à colorier plus de la moitié de la grille de jeu, en partant
de sa case de départ : coin supérieur gauche pour le joueur A, coin inférieur
droit pour le joueur B.
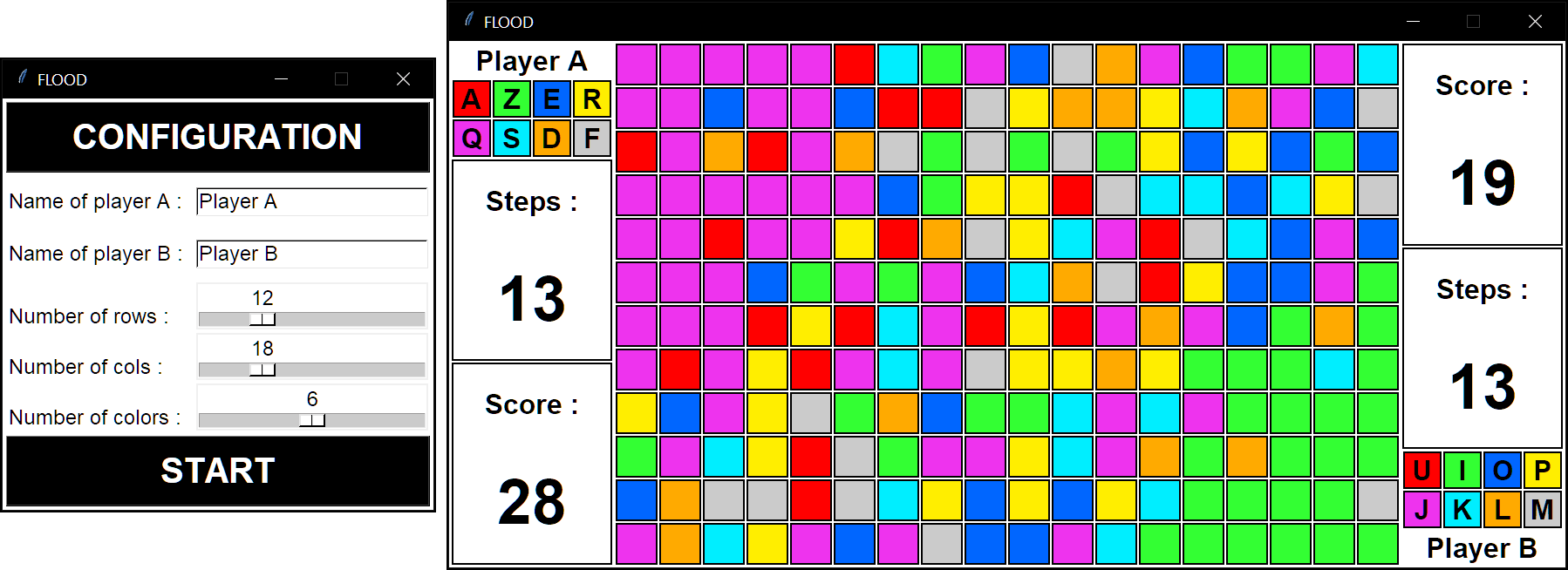
La figure ci-dessous fournit un exemple possible pour l'interface graphique du
programme. Dans un premier temps, on affiche une fenêtre de configuration (cf.
à gauche de la figure) permettant de saisir les différents paramètres du jeu
(noms des joueurs, taille de la grille, nombre de couleur pour les cases). Puis,
lorsque le joueur clique sur le bouton 'START', la fenêtre de configuration
est remplacée par la fenêtre principale du jeu (cf. à droite de la figure), qui
se compose de 3 zones : la zone centrale montre la grille de jeu, commune aux
2 joueurs, et les zones droite et gauche affichent les informations relatives
à chaque joueur.
 Pour effectuer le choix des couleurs à utiliser à chaque coup, les 2 joueurs se
partagent le clavier : le joueur A utilise la partie gauche du clavier (touches
A,Z,E,R,Q,S,D,F) et le joueur B, la partie droite (touches U,I,O,P,J,K,L,M). Un
aide-mémoire est affiché sur la zone de chaque joueur pour lui rappeler les
couleurs associées aux différentes touches qui le concerne. De même, la
progression de la partie est visualisée en affichant le nombre de coups joués,
ainsi que le score courant pour chacun des 2 joueurs (correspondant au nombre
de cases coloriées lors du dernier coup).
Pour effectuer le choix des couleurs à utiliser à chaque coup, les 2 joueurs se
partagent le clavier : le joueur A utilise la partie gauche du clavier (touches
A,Z,E,R,Q,S,D,F) et le joueur B, la partie droite (touches U,I,O,P,J,K,L,M). Un
aide-mémoire est affiché sur la zone de chaque joueur pour lui rappeler les
couleurs associées aux différentes touches qui le concerne. De même, la
progression de la partie est visualisée en affichant le nombre de coups joués,
ainsi que le score courant pour chacun des 2 joueurs (correspondant au nombre
de cases coloriées lors du dernier coup).
Une caractéristique importante du jeu est que la partie ne se déroule pas en
mode tour-par-tour, mais en mode temps-réel, donc rien n'interdit à un joueur
d'effectuer rapidement plusieurs coups d'affilée sans que l'adversaire ne joue.
Néanmoins, un joueur n'a droit qu'à un nombre limité de coups pour chaque
partie (ce nombre est calculé en fonction de la taille de la grille et du
nombre de couleurs). Lorsque la réserve de coups d'un joueur est épuisée,
l'adversaire peut continuer à jouer pour augmenter sa conquête territoriale. A
l'inverse, le jeu se bloque dès que l'un des joueurs a réussi à colorier plus
de la moitié des cases de la grille, et le programme affiche le vainqueur de la
partie.
De manière optionnelle, on peut également intégrer dans le programme, un
mécanisme de sauvegarde/récupération des parties jouées. Pour cela, l'idéal est
d'utiliser un fichier au format INI tel qu'on l'a vu en cours. Il n'y a pas de
directives spécifiques pour le format exact de ce fichier, à vous d'imaginer un
formalisme permettant de stocker et récupérer facilement toutes les
informations d'une partie donnée (date et heure, noms des joueurs, taille de la
grille, nombre de couleurs, liste des coups joués et score final)
Pour simplifier le développement du programme, on fournit une archive flood.zip qui contient un fichier
squelette floodZ.py qui pourra servir de point de départ pour
l'implémentation.
Exemples à relire avant de commencer le projdet :
- Page Wikipedia concernant
le remplissage par diffusion qui est l'algorithme principal à implémenter
pour effectuer le changement de couleur des cases.
- Exemple C5C_win.py (pour l'alternance entre fenêtre de configuration et
fenêtre de jeu)
- Exemple C2C_toggle.py (pour le changement d'état automatique des case de la grille)
- Exemple C6D_event.py et Exercice C6A_slide.py (pour la gestion
des touches du clavier)
- Exemple B5A_inifile.py et B6_scores.py (pour la lecture/écriture des fichiers INI)
Projet 3 : Bridges
Ecrire un programme bridges qui implémente le jeu
de connexions, originaire du Japon, sous le nom de Hashiwokakero (cf.
cette page Wikipedia
pour avoir toutes les informations sur les règles du jeu). L'objectif du joueur
est de connecter l'ensemble des îles placées sur une grille, en construisant le
nombre exact de ponts indiqué pour chaque île. Une version jouable en ligne se
trouve sur ce site et
permet de se familiariser au mécanisme du jeu avec des exemples de complexité
variable.
Dans la version originale, chaque île ne peut être connectée que par 1 ou 2
ponts avec chacune de ses 4 îles voisines (N, E, S, W). Pour augmenter la
difficulté du jeu, la variante implémentée pour ce sujet autorise 1, 2 ou 3
ponts dans chacune des 4 directions, mais en imposant un nombre maximal de 9
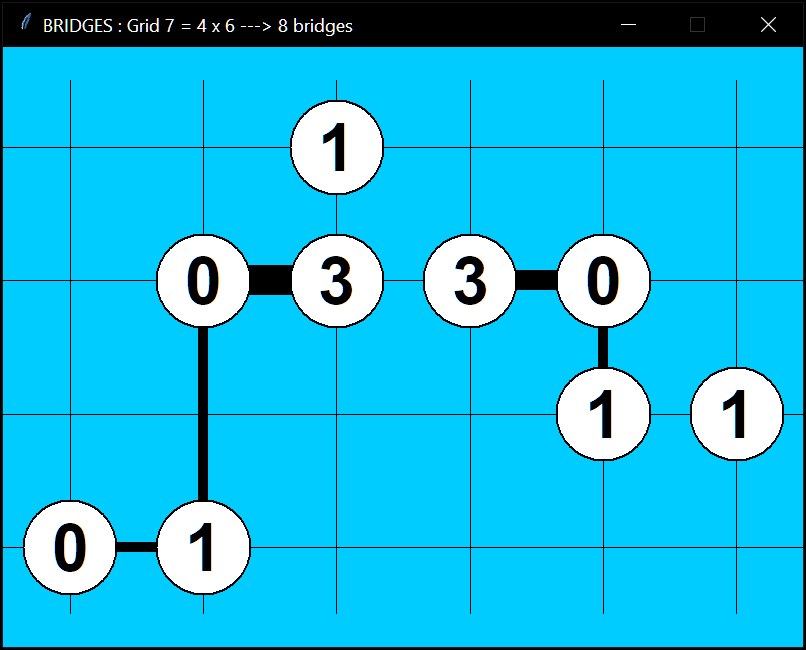
ponts pour chacune des îles. De plus, pour simplifier la fonction d'affichage,
on ne visualise les ponts que par un seul segment entre deux îles, mais dont
l'épaisseur sera variable (trait fin pour un pont simple, trait moyen
pour un pont double, trait épais pour un pont triple). La figure ci-dessous
fournit un exemple possible pour l'interface graphique du programme, dans lequel
on peut voir les 3 épaisseurs des ponts reliant les îles.
 L'interaction entre le programe et le joueur s'effectue uniquement à l'aide
de la souris. Lorsque le joueur clique sur une première île, celle-ci devient
"active" (ce qui sera symbolisé par un changement de couleur du disque associé
à l'île), puis en cliquant sur une des îles voisines, un pont sera créé avec
un segment d'une épaisseur variable selon le nombre de clics. Si le joueur
réalise qu'il s'est trompé, il peut détruire un pont entre 2 îles en cliquant
avec le bouton droit au lieu du bouton gauche. Au fur et à mesure de la
création ou destruction des ponts, les compteurs sur les îles sont décrémentés
ou incrémentés. Par conséquent, lorsque tous les compteurs tombent à la valeur
0, le niveau est considéré comme résolu et le programme doit afficher le niveau
suivant.
L'interaction entre le programe et le joueur s'effectue uniquement à l'aide
de la souris. Lorsque le joueur clique sur une première île, celle-ci devient
"active" (ce qui sera symbolisé par un changement de couleur du disque associé
à l'île), puis en cliquant sur une des îles voisines, un pont sera créé avec
un segment d'une épaisseur variable selon le nombre de clics. Si le joueur
réalise qu'il s'est trompé, il peut détruire un pont entre 2 îles en cliquant
avec le bouton droit au lieu du bouton gauche. Au fur et à mesure de la
création ou destruction des ponts, les compteurs sur les îles sont décrémentés
ou incrémentés. Par conséquent, lorsque tous les compteurs tombent à la valeur
0, le niveau est considéré comme résolu et le programme doit afficher le niveau
suivant.
Pour simplifier le développement du programme, on fournit une archive
bridges.zip qui contient un fichier CSV
regroupant 1000 grilles de taille variable, classées par niveau de difficulté,
ainsi qu'un fichier squelette bridgesZ.py qui pourra servir de point de
départ pour l'implémentation. La lecture du fichier CSV et sa conversion en un
tableau de listes sont déjà inclus dans le squelette.
Exemples à relire avant de commencer le projet :
- Exemple C7A_canvas.py (pour l'utilisation générale de la widget Canvas)
- Exemple C7D_canvas.py (pour la détection des éléments cliqués dans un Canvas)
- Exemple B4A_csvfile.py et Exercice C6A_maze.py (pour la lecture des
fichiers CSV)
Projet 4 : Automates cellulaires
Ecrire un programme autocell qui permet de visualiser
de manière graphique, l'évolution temporelle de différents modèles d'automates
cellulaires. Les automates cellulaires constituent les structures les plus
simples utilisés pour les algorithmes de simulation de "vie artificielle" (cf.
cette page
Wikipedia pour avoir des informations sur les principes de mise en
oeuvre, ainsi que sur les différents modèles proposés dans ce contexte).
Parmi ces modèles, le Jeu de la Vie, inventé en 1970 par le mathématicien
John Conway, est sans conteste l'automate cellulaire le plus célèbre. L'ensemble
de ses caractéristiques sont présentés de manière extrêmement détaillée sur le
site conwaylife.com.
Un automate cellulaire est généralement défini sur une grille 2D, dans laquelle
chaque cellule de la grille va évoluer au cours du temps, en fonction de la
configuration de son voisinage. Plus précisément, chaque automate est défini
par 3 paramètres : states = le nombre d'états possibles pour chaque
cellule, peers = la liste des cellules voisines à prendre en compte pour
contrôler l'évolution d'une cellule, et rules = un ensemble de règles de
transition pour définir chacune des configurations permettant à une cellule de
passer d'un état X vers un état Y.
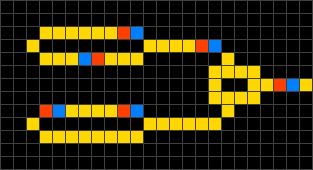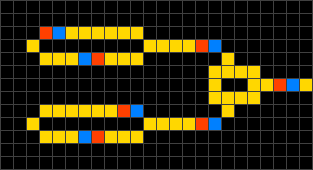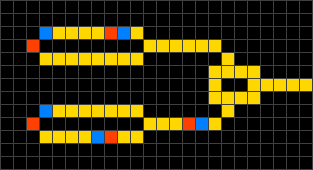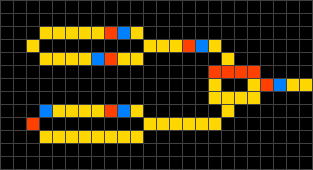

A titre d'exemple, l'image de gauche de la figure ci-dessus montre une
animation du modèle
WireWorld qui a
été développé pour simuler le comportement des circuits électriques. Dans le
cadre de ce projet, ce modèle sera défini par un dictionnaire Python (cf.
code ci-dessous) contenant les valeurs associées aux 3 paramètres
states, peers et rules. Pour ce modèle, chaque cellule
peut prendre un des 4 états possibles (A, B, C ou D), symbolisés par des
couleurs (A = noir = vide, B = jaune = conducteur électrique, C = bleu = début
du signal, D = rouge = fin du signal). Les cellules voisines à prendre en
compte pour l'évolution d'une cellule sont identifiées par un ensemble de 8
vecteurs de translation, permettant de trouver les coordonnées des 8 cases
voisines. Et enfin, les différentes règles de transition sont spécifiées par
une liste de couples, où chaque couple est composés d'une chaîne de 2
caractères (représentant respectivement l'état initial et l'état final de la
transition considérée) et d'un dictionnaire (décrivant la configuration
nécessaire du voisinage pour activer cette transition). Par exemple la règle
'AA',{} signifie qu'une cellule dans l'état A (case noire) va
rester dans l'état A, quelque soit la configuration de son voisinage (on peut
effectivement constater sur l'animation, que les cases noires ne changent
jamais de couleur). De même, la règle 'BC',{'C':{1,2}} signifie
qu'une cellule va passer de l'état B (case jaune) à l'état C (case bleue) dès
qu'il y a 1 ou 2 cellules, parmi ses 8 voisins, qui sont dans l'état C. Par
convention, les règles de transition sont toujours ordonnées par rapport à
l'état initial, et s'il y a plusieurs règles qui s'appliquent à un même état
initial, celles-ci sont systématiquement classées de la plus spécifique à la
plus générique. Ainsi, pour l'automate WireWorld, la règle 'BB':{}
ne s'appliquera que si la règle 'BC':{'C':{1,2}}
a échoué.
wireworld = {
'states': 'ABCD',
'peers': [(-1,0),(1,0),(0,-1),(0,1),(-1,-1),(-1,1),(1,-1),(1,1)],
'rules': ['AA',{}, 'BC',{'C':{1,2}}, 'BB',{}, 'CD',{}, 'DB',{}]
}
L'image de droite de la figure montre une animation résultant d'un
autre modèle classique d'automate cellulaire, appelé
Greenberg-Hastings, dont l'intérêt principal est de permettre de
simuler la propagation de certaines réactions chimiques dans les fluides.
Pour simplifier le développement du programme, on fournit une archive
autocell.zip qui contient d'une part
un fichier automata.py regroupant les paramètres de définition de 9
modèles classiques d'automates cellulaires, et d'autre part, le fichier
automata.ini qui contient, pour chacun de ces 9 modèles, quelques
exemples de configurations initiales permettant d'obtenir des évolutions
intéressantes lors de la simulation. L'objectif du projet sera donc de lire
ces fichiers de données, de permettre à l'utilisateur de choisir un
modèle d'automate et une configuration initiale, puis de visualiser
graphiquement l'évolution de la grille au cours du temps, en appliquant les
règles de transition adéquates pour chacune des cellules en fonction de son
voisinage. On pourra évidemment rajouter d'autres modèles d'automates ou des
configurations initiales personnalisées ; la seule contrainte étant de rester
dans le même formalisme de description. De même, toutes les améliorations de
l'interface permettant d'apporter des fonctionnalités supplémentaires seront
les bienvenues (on pourra librement s'inspirer de ce qui est proposé sur le
site conwaylife.com déjà cité plus
haut). Dernière remarque : pour gagner en vitesse d'affichage (notamment
lorsque le nombre de cellules est important) il est fortement conseillé
d'afficher la grille via une widget Canvas au lieu d'un ensemble de
widgets Brick.
Exemples à relire avant de commencer le projet :
- Exemple C7A_canvas.py (pour l'utilisation générale de la widget Canvas)
- Exercice C8A_maze.py (pour l'affichage d'une grille dans un Canvas)
- Exemple B5A_inifile.py (pour la lecture des fichiers INI)
Philippe Blasi